Maxsus çağıştırmalılıq teoriäse
Çağıştırmalılıq teoriäse yä Maxsus çağıştırmalılıq teoriäse - 1905 yılda bastırılğan Albert Einstein'nıñ fizik teoriäse, İsaak Nyuton fizikasın almaştırdı, elektromagnitizm Makswell tigezlämäläre yärdämendä kürsätelän. Bu teoriä maxsus atlı, çönki çağıştırmalılıqnıñ Einstein mäsläklärendä tartılu köçe qaralmağan. Un yıldan soñ Einstein Ğomumi çağıştırmalılıq teoriäsen bastırıla, bu teoriägä tartılu köçe kertelgän.
Maxsus çağıştırmalılıq teoriäseneñ dälilläre[үзгәртү | вики-текстны үзгәртү]

Çağıştırmalılıq mäslägen Galileo Galiley kertä. Aristotelneñ qaraşın yuqqa çığarğaç, ul şunnan ğibarät bula: xäräkät, tigez turı xäräkät ayıruça, berär närsägä çağıştırmaça bula, absolüt başlap sanaw sisteması bula almıy. Galileo xäzerge zamannarda da yaraqlı Galileo tigezlämälären kertä. Galileo xäräkätneñ biş qanunın kertä. Newton anı yaxşırtıp, xäräkätneñ öç qanunın ğına qaldıra.
Bu qanunar qatı cisemnär öçen eşlilär, yaqtılıq öçen alar eşlämilär. Newton'ça yaqtılıq tabiğäte - kisäkçeklär ("korpuskulär") ide, soñraq fiziklär "arqılı dulqınnar modele" qullanışlıraq bulu fikeregä kilälär. Mexanik dulqınnar moxitta küçälär, yaqtılıq öçen dä şundıy model qullana başlıylar. Bu gipotetik moxit "äfer" (efir) isemen ala. "Äfer"dä ber-bersenä qarşı kilüçe parametrlar da bar: dulqın tizlege zur bulu öçen ul bik tığız bulırğa tieş, ämmä bu tığızlıq Cirne tuqtatırğa tieş tügel. Bu fiker - absolüt sanap başlaw sisteması fikerenä oxşaş, ämma monda äfer absolüt sistemasınıñ başı bula.
19 ğasırdän yaqtılıq, elektr häm magnetizm'nıñ elektromagnit qırı aspektları añlaşılırğa başlıylar. Maxwell'nıñ tigezlämälär buyınça tizlätüçe qorılmalar yaqtılıq tizlege belän cäyelüçe elektromagnit nurlaşunı çığara. Tigezlämälär nurlaşu tizlegeneñ çığanaqnıñ tizlegennän bäysezlegen kürsätälär. Bu mexanik dulınnarğa oxşaşlığınnan kilep çığa. Mixelson-Morley eksperimentınnan soñ şundıy nätcägä kitälär: nurlaşuınıñ tizlege çığanaq tizlegenä häm küzätüçe tigezlegenä bäyle bulmıy, ul invariant ide.
Hendrik Lorentz häm başqalar elektromegnit köçlärenneñ küzätüçe urnaştıruına bäylelärne kürep alalar. Ber sistemada berençe toruçı küzätäçe ber ölkäsendä qırnı "kürmi", ä ikiençese xäräkätläderüçe küzätäçe "kürä". Lorentz statsionar äfer çağıştırmaça xäräkäte Lorentz-Fitzgerald qısqartması teoriäse nigezenä sala. Soñraq bu teoriäne qatı täñqit itälär.
Lorentz üz transformasiäse tigelämälären täqdim itsä dä, Eynşteyn'nıñ kertelgän öleşe bu tigezlämlär bigräk tä fundamental teoridän çığaru. Bu teoriä äferneñ qarşılıqnı taläp itmi. Eynşteyn närsä bar küzätüçegä invariant bula belän qızıqsına. Maxsus çağıştırmalılıq buyınça Lorentz-Fitzcerald'nıñ qatlawlı toyılğan transformasiälär ğädi geometriädän häm Pifagor teoremmalarınnan çığarıla. Bu teoriäneñ original iseme (Almançadan tärcemä itelgän) "İnvariantlar Teoriäse". Maks Plank "çağıştırmalılıq" terminen täqdim itä, çönki teoriäneñ fikerläwendä ike küzätüçelär ber bergä çağıştırılmaça xäräkätlänälär.
Maxsus çağıştırmalılıq tuqtawçı häm tigez tizlege belän xäräkätlänüçe (inertsial başlap sanaw sistemasındä buluçı) cisemnär öçen qullanalar, ğädättä. Törle inertsial başlap sanaw sistemasındä terkäp quyğan cisemneñ urınlaştırıluı häm tigezlege Lorentz transformatsiäse tigezlänäläre aşa täñgäl kilälär. Şunnan zur ğomumi xata çığarıla: maxsus çığıştımalılıq tizläneş belän xäräkätlänüçe cisemnärgä dä qullanırğa bulmıy, dilär. Bu yalğış. Mäsälän, relätivistik raket mäsäläse. Maxsus çağıştırmalılıq daimi gravitatsion qırında tizläneş belän xäräkät itüçe häm äylänüçe başlap sanaw sistemasendä buluçı cisemnär öçen xäräkätlär farazlanırğa bula. Ämmä almaşınuçan gravitatsion qırındağı cisemnärneñ xäräkätlären ciñel häm matur taswirlap birä almıybız.
Maxsus çağıştırmalılıq teoriäse postulatları[үзгәртү | вики-текстны үзгәртү]
1. Berençe postulat (çağıştırmallılıq postulatı)
- Törle inertsial küzätüçelär fizik küreneşlär küzätülärneñ näticäläre üz-üzenä häm real täbiğät küreneşenä yaraşırğa tieş. Yäğni, Ğälämneñ sıyfatları inertsial küzätäçeneñ urınlaştırılına bäyle bulmıy.
- Här inertsial küzätüçe öçen här fizik teoriä metematikçä bertörle.
2. İkençe postulat (c-nıñ daimilege)
- Vakuumda yaqtılıq tizlege (c) böten inertial küzätüçelärgä bertörle, böten yünäleşlärgä bertörle, çığanaqnıñ häm küzätüçeneñ tizlegenä bäyle bulmıy. Eksperimentalçä tikşertkän. Berençe häm İkençe postulattan şundıy sözemtä ide: yaqtı taratu öçen bernindi moxit ("äfer" dä) kiräkmi.
Postulatlarnıñ matematik yazması[үзгәртү | вики-текстны үзгәртү]
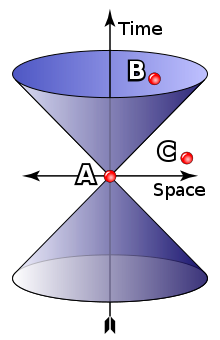
Maxsus çağıştırmalılıqnıñ tögäl matematik yazmasında bez 4-ülçämle waqıt-fäzanı M (Minkowski fäzası) qullanabız. Bu sistemdäge noqtalar - waqiğalar idelär; fizik cisemnär şundıy fäzada sızıqlar (cisem noqta bulsa) yä kisäklär (cisem noqta bulmıyça). Sızıqlar yä kisäklär cisemneñ xäräkäten taswirlap birälär; cisemdä başqa fizik sıyfatlar da bar: energiä, moment, massa, qorılma, h.b..
İnertsial küzätüçe terminnı qullanabız. Här inertsial küzätäçedä üz inertsial başlap sanaw sisteması bar. Bu sistema M fäzası waqiğalarına koordinatlar sisteması bula. Bu başlap sanaw sisteması başqa fizik sıyfatlarına koordinatlar birä. cisemneñ moment häm energiä öçen, electromagnit qır öçen, h.b..
Birelgän berar nindi ike inertial küzätüçe, berençe başlap sanaw sistemasınnan ikençegä äwerelüçe koordinatlar transformatsiäse. Bu transformasiä koordinatlarğa genä tügel, böten fizik koordinatlar öçen yaraqlı ide: moment häm energiä , h.b.. Transformasiä qanunnarın tenzor matematikasınnan çığarırğa bula.
Här fizik qanun inertsial başlap sanaw sistemasınıñ koordinatlarında yazılğan tigezlämälär (differentsial tigezlämälär dä) sistemasında yazılırğa bula. Bu tigezlär waqıt-fäzasında törle cisemnärene törle koordinatlarğa bäylä. Ürnäklär: Makswell tigezlämäläre, Newton'nıñ berençe qanunı.
1. Berençe Postulat (Çağıştırmalılıq prinsibe)
- Här fizik qanun inertsial koordinatlar transformasiälardan soñ invariantlı qala.
2. İkençe Postulate (c-nıñ daimilege)
- şundıy ısulı belän bilgelängän absolút konstant bar bula. Ägär A, B isemle inertsial başlap sanaw sistemında häm koordinatlı ike waqiğa ikençesedä ( isemle) häm koordinatlar bulsalar,
- häm bulsa genä.
İkençe Postulat raslawınça, ber başlap sanaw sistemendä c tizlekle cisem başqalarda tağın c tizlege belän xäräkät itä. İkençe Postulat Berençedän häm Maxwell'neñ tigezlämälärdän matematikçä çığarıla ikän, şundıy oçraqta c şulay çığara: . Çönki Maxwell'neñ tigezlämälär electromagnit nurlaşuın yaqtı kebek yörtä, c-nı yaqtılıq tizlege bularaq qullanalar.
İkençe Postulatnı anıñ üzeneñ tögelräk yuraması qullanırğa bula. Fäza-waqıt intervalı inertsial başlap sanaw sistemlären alışqaç, invariant bulıp qala. Berar nindi A häm B waqiğalar öçen:
ide. Başlap sanaw sistemeläre arasında transformasiäları öçen qanunnar çağıştıru bu qanun qullanırğa bula; Lorentz transformasiälären qara.
Pseudo-Rieman küptabaqlı fäzasın qullanğaç, Postulatlarnıñ matematik küzallawı qısqarala.
Galileo çağıştırmalılığı - maxsus çağıştırmalılıqnıñ non-relätivistik limitçä töre . Bu teoriädä berençe postulat üzgärmä, ikençe postulat şulay üzgärä:
- Ägär A, B waqiğalarda isemle inertsial başlap sanaw sistemasında häm koordinatları häm başqa inertsial sistemasında () häm koordinatlar bulsa, ide. Ägär da bulsa,
- ide.
Klassik mexanika häm Newton'nıñ tartılışı Galileo çağıştırmalılığı belän ezlekle bula, ämma maxsus çağıştırmalılıq belän ezlekle bulmıy. Kiresençä, Maxwell'neñ tigezlämäläre Galileo çağıştırmalılığı belän elekle bulmıy (fizik äferneñ buluın iğlan itüçe postulattan başqa). Oçraqlarnıñ küpçelegendä maxsus çağıştırmalılıqta fizik qanunar (härkemgä mäşhür dä) maxsus şağıştırmalılıqnıñ postulatlardan häm non-relätivistik limitlarda qullanılğan maxsus çağıştırımalılıq qanunnar klassik mexanikaça başqarılğan gipotezasınnan çağırıla.
Maxsus çağıştırmalılıqnıñ statusı[үзгәртү | вики-текстны үзгәртү]
Maxsus çağıtırmalılıq teoriäsen böten fizik cämäğät qabul itä. Teoriägä qarşı eksperiment näticäläre xata bulıp sanalalar. Ğomumi çağıştırmalılıq teoriäse eksperimentlarga täñgäl kilä, şunlıqtan gravitatsiäneñ başqa teoriälärgä (Brans-Dik teoriäse kebek) yul qardırmıy.
Maxsus çağıştırmalılıqnıñ näticäläre[үзгәртү | вики-текстны үзгәртү]
- İke waqiğa waqıt arası invariant bulmıy, bu ara küzätüçelärneñ başlap sanaw sistemalarınıñ çağıştırma tizlegenä bäyle. (Lorentz transformasiä tigezlämälären qara)
- Ber başlap sanaw sistemasında ber ük waqıtta bulğan ike waqiğa başqa sistemasında törle waqıtlarda bula alalar (sinxronlıq).
- Ber cisemneñ ozınlığı törle küzätüçedä törle bulıp ala. (Lorentz transformasí tigezlämälären qara)
- İgezäklär paradoksı: kosmosta yaqtı tizlegenä yaqınnan oçuçı ber igezäk, Cirgä qaytqaç, üze bertuğanı üzennän tizräk qartayğan tabaçaq.
Absolüt başlap sanaw sisteması bulmaw[үзгәртү | вики-текстны үзгәртү]
Maxsus çağıştırmalılıq buyınça absolüt başlap sanaw sistema bula almıy; böten daimi tizlekle küzätüçelär çağıştırmaça böten fizik qanunnarı bertörle başqarılırğa tieş.
Massa, moment häm energiä[үзгәртү | вики-текстны үзгәртү]
Bu metodlar moment häm energiä bilgeläw öçen qullanalar.
Birelgän M massalı v tizlege belän baruçı cisem. Energiä häm momentnı şulay itep çığarabız:
γ - (Lorentz koeffitsientı):
c - yaqtı tizlege. Energiä häm moment şulay bäylängän:
- relátivistik energiä-moment tigezläre.
Küp tapqır keçeräk tizleklär öçen Taylor räte belän approksimatsiä itelgän γ-nı qullanırğa bula:
Bu formulalar Newton'ça kinetik energiägä häm momentqa elekle. Maxsus çağıştırmalılıq tübän tigezlärdä Newton mexanikasına elekle.
Şundí formulalardan ber cisem xäräkät itmäsä, (v = 0 häm γ = 1) nul-energiä çığarıla:
Bu xäräkätsezle energiä ide. Bu Newton teoriägä qarışma, çönki ul daimi ide.
Bu formula buyınça çağıştırmalılıqta mass energiäneñ başqa töre ide. TBu formula atom-töş massaları öçen bik möhim. Massnıñ arasına kürgäç, bez atom-töş reaksínıñ energiäne farazlana alabız. Bu formula XX ğasırnıñ fizik açıqlarınıñ iñ möhime.
Massa[үзгәртү | вики-текстны үзгәртү]
Çağıştırmalılıqta massanıñ ike bilgelämä qullanıla. Berençese: invariant massa yä xäräkätsezle mass. Bu massa böten inetsial başlap sanaw sistemalarında daimi ide. Bu massa tizlekkä bäyle bulmıy.
İkençese relätivistik massa ide:
Relátivistik mass γ-gä bäyle bula, çönki
böten başlap sanaw sistemalarında yaraqlı. Tizlek nul bulsa relátivistik häm inertsial massalar bertigez bulalar.
Relátivistik massa skalár tügel (törle küçärlärdä ul törle ide).
Maxsus çağıştirmalılq postulatlarınıñ testläre[үзгәртү | вики-текстны үзгәртү]
- Mixelson-Morley eksperimentı - äfer cile
- Hamar experimentı - äfer taşqını öçen kirtä
- Trouton-Nobl experimentı - kondensatornıñ äylänmä momentı
- Kennedi-Torndayk experimentı - waqıtnıñ qısuı
- Nurlaşu teorise experimente
Monı da qara[үзгәртү | вики-текстны үзгәртү]
- Keşelär: Arthur Eddington | Albert Einstein | Hendrik Lorentz | Hermann Minkowski | Bernhard Riemann | Henri Poincaré | Alexander MacFarlane | Robert S. Shankland
Sıltamalar[үзгәртү | вики-текстны үзгәртү]
- Reflections on Relativity A complete online book on relativity
- http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Special_relativity.html 2006 елның 8 ноябрь көнендә архивланган.
- Brane World Mach Principles and the Michelson-Morley experiment 2006 елның 28 сентябрь көнендә архивланган.
- Why Hyperspace & Dual Reference frames
- Special Relativity: a matter of perspective Special relativity presented as a natural 4D extension of perspective
- Petites expériences de pensée .
- Special relativity theory made intuitive : a new approach to explain the theoretical meaning of Special Relativity from an intuitive geometrical viewpoint
| Bu mäqälä Tatar (Latin) Wikipediäseneñ saylangan mäqälälär rätenä kerä. |




























