Mäydan

Mäydan - geometrik ike ülçäneşle figura (yassı yä käkre) san sıyfatlaması, figuranıñ zurlığın kürsätä.
Tarixında mäydan xisaplaw kvadratura dip yörtelä.
Mäydanğa iä buluçı figura - kvadraturalı dip isemlänä.
İntegral' isäpläw geometrik figuralarnı ğomumi xisaplaw ısulın birä.
Mäydan üzlekläre[үзгәртү | вики-текстны үзгәртү]
- Uñaylıq
- Additivlek - figuranıñ mäydanı eçke figuranıñ öleşläre summasına tigez
- İnvariantlıq - kongruent figuralarınıñ mäydannarı bertigez
- Normalaştırlıq - ber-yaqlı kvadrat mäydanı bergä tigez.
Mäydannı xisaplaw matematik ısullar[үзгәртү | вики-текстны үзгәртү]

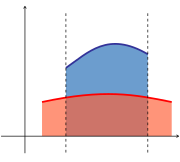
Funktsiä grafigı häm gorizontal' küçär arasında mäydan intervalında kiläse integralğa tigez:
İke funktsiä grafigı arasında mäydan:
Polär koordinatlar[үзгәртү | вики-текстны үзгәртү]
Polär koordinatlarda mäydan:
- .
Öslek mäydanı[үзгәртү | вики-текстны үзгәртү]
yäki tulı koordinatlarda
- biredä .
Metrik berämleklär[үзгәртү | вики-текстны үзгәртү]
- Kvadrat kilometr 1 km² = 1 000 000 m²
- Gektar 1 ga = 10 000 m²
- Ar 1 a = 100 m²
Ädäbiät[үзгәртү | вики-текстны үзгәртү]
- Энциклопедия элементарной математики. Книга пятая. Геометрия / под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М.: Наука, 1966. — 624 с.
- Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2
- История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени.
- История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. II: Математика XVII столетия.
- Boyer C. B., Merzbach U. C. A History of Mathematics. — John Wiley & Sons, 2010. — 640 p

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





