Karl Fridrix Gauss
| Karl Fridrix Gauss almança Carl Friedrich Gauß | |
|---|---|
 Karl Fridrix Gauss | |
| Tulı iseme | Johann Carl Friedrich Gauß |
| Hönäre | matematik, mexanik, fizik, astronom, geodezist |
| Tuu datası | 30 aprel 1777 |
| Tuu cire | Braunşweig, Almaniä |
| Watandaşlığı | Almaniä |
| Ülem datası | 23 fevral 1855 (77 yäş) |
| Ülem cire | Göttingen |

İohann Karl Fridrix Gauss (almança Johann Carl Friedrich Gauß; 1777-1855, Göttingen) - alman matematigı, mexanik, fizik, astronom, geodezist.
Dönya tarixında iñ mäşhür matematiklarnıñ berse bulıp sanala. Kolli medale laureatı, Şved, Rusiä Fännär Akademiäseneñ çit il äğzası.
Tärcemäi xäle[үзгәртү | вики-текстны үзгәртү]

1777 yılda Gauss krestian ğailäsendä Braunşweig hertsoglığında tuğan.
1792-1795 yılda Bartels yärdämendä Kollegium Karolinum köliätendä uqığan.
1795-1798 yılda Göttingen Universitetında uqıy.
1798 yılda Gauss üz şedevrın "Arifmetik tikşerenülär" kitabın yazıp beterä, 1801 yılda bastırıp çığarıla. Bu kitapta "Matematika - fännär patşası, ä sannar teoriäse - matematikanıñ patşası" - digän süzlär bar.
1799 yılda Algebranıñ töp teoremasın isbatlağan.
1801 yılda Peterburg Fännär Akademiäseneñ äğzası itep saylana.
1807 yılda Napoleon ğäskärläre Göttingen şähären basıp ala, şähärneñ watandaşlarına zur kontributsiä salına, Gauss 2000 frank tülärgä mäcbür itä.
1809 yılda "Küktäge cisemnärneñ xäräkät teoriäse" kitabın yaza.
1811-1812 yılda kompleks sannarı häm gipergeometrik rät belän eşli.
1821 yılda öslek teoriäse belän eşli başlıy, Gauss käkrelegen töşençäsen kertä, differentsial' geometriägä nigez sala.
1825 yılda gauss kompleks sannarın aça.
1832 yılda "Bikvadrat alımnar teoriäse" kitabın yaza.
1833 yılda Gauss elektrik telegrafnı uylap çığara (Weber bergä) häm tözi.
1839 yılda urıs telen öyränä, Lobaçevskiy eşläre belän qızıqsına.
1842 yılda Gauss täqdime buyınça Lobaçevskiy Göttingen patşa cämğiäteneñ äğza-korrespondentı itep saylana.
1839 yılda Gauss Potentsial teoriäsen tiränten tikşerä, elektrostatikanıñ baş teoremasın "Gauss teoreması"n isbatlıy.
1855 yılda Gauss Göttingen şähärendä ülgän.
Fänni qazanışları[үзгәртү | вики-текстны үзгәртү]
Algebranıñ töp teoreması[үзгәртү | вики-текстны үзгәртү]
Härber konstanta bulmağan küpbuın (ber argument belän) belän kompleks koeffitsientlar - kompleks sannarınıñ qırında içmasam ber tamırğa iä bula.
Gauss büleneşe[үзгәртү | вики-текстны үзгәртү]
Gauss büleneşe yäki Normal' büleneş - ixtimallıq büleneşe, ber ülçäneşle oçraqta büleneş tığızlığı f(x) belän taswirlana:
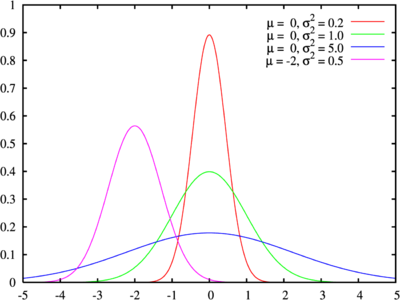
Gauss teoreması[үзгәртү | вики-текстны үзгәртү]
- Gauss teoreması: Gauss qanunı külämdäge qorğı häm Elektr qırı köçäneşlelegeneñ ağımı arasında bäyläneşen kürsätä.
SGS
Si
biredä:
- — Elektr qırı köçäneşlelegeneñ ağımı yomıq S öslege aşa
- — tulı qorğı külämdä
- Differentsial' küreneş
SGS:
Si:
Ostrogradskiy-Gauss tigezlämäse[үзгәртү | вики-текстны үзгәртү]
- Ostrogradskiy-Gauss tigezlämäse, vektor qırınıñ ağımı:
yä
Öç ülçäneşle fäzada :
yäki
Äsärläre (rusça)[үзгәртү | вики-текстны үзгәртү]
- Гаусс К. Ф. Избранные геодезические сочинения. Т. 1. — М.: Геодезиздат, 1957.
- Гаусс К. Ф. Исследования по оптике. — НИЦ «Регулярная и хаотическая динамика», 2011. — ISBN 978-5-93972-871-3.
- Гаусс К. Ф. Общие исследования о кривых поверхностях // Основания геометрии (сб.). — М.: ГИТТЛ, 1956.
- Гаусс К. Ф. Отрывки из писем и черновиков, относящиеся к неевклидовой геометрии. // Основания геометрии (сб.). — М.: ГИТТЛ, 1956.
- Гаусс К. Ф. Пояснение возможности построения семнадцатиугольника // Историко-математические исследования. — М.: Наука, 1976. — № 21. — С. 285—291.
- Гаусс К. Ф. Труды по теории чисел. Перевод Б. Б. Демьянова, общая редакция И. М. Виноградова, комментарии Б. Н. Делоне. — М.: Изд-во АН СССР, 1959.
Ädäbiät[үзгәртү | вики-текстны үзгәртү]
- Белл Э. Т. Творцы математики. — М.: Просвещение, 1979. — 256 с.
- Боголюбов А. Н. Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
- Бюлер В. Гаусс. Биографическое исследование. — М.: Наука, 1989. — 208 с. — ISBN 5-02-013919-X.
- Гаусс К. Ф.: Сб. статей под ред. И. М. Виноградова (к 100-летию со дня смерти). — М.: АН СССР, 1956. — 312 с.
- Гиндикин С. Г. Рассказы о физиках и математиках. 3-е изд. — М.: МЦНМО, 2001. — ISBN 5-900916-83-9.
- Голубев Ю. Ф. Основы теоретической механики. — М.: Изд-во МГУ, 2000. — 719 с. — ISBN 5-211-04244-1.
- Колмогоров А. Н., Юшкевич А. П. (ред.) Математика XIX века. Т. 1. Математическая логика. Алгебра. Теория чисел. Теория вероятностей. — М.: Наука, 1978.
- Колмогоров А. Н., Юшкевич А. П. (ред.) Математика XIX века. Т. 2. Геометрия. Теория аналитических функций. — М.: Наука, 1981.
- Маркеев А. П. Теоретическая механика. — М.: Наука, 1990. — 416 с. — ISBN 5-02-014016-3.
- Моисеев Н. Д. Очерки истории развития механики. — М.: Изд-во Моск. ун-та, 1961. — 478 с.
- Тюлина И. А. История и методология механики. — М.: Изд-во Моск. ун-та, 1979. — 282 с.
- Храмов Ю. А. Физики. Биографический справочник. — М.: Наука, 1983. — 400 с.













