Функция чыгарылмасы

Функция чыгарылмасы

Функция чыгарылмасы (ноктада) — билгеләнгән ноктада функция үзгәреше тизлеген тасвирлаучы дифференциаль хисапның төп төшенчәсе.

Функция чыгарылмасы — функция артымы аргумент артымына чагыштырмасының чиге булып билгеләнә (аргумент һәм функция артымнары нульгә омтылалар).

Чикле чыгарылмасына ия булган функция ноктада дифференциаль функция дип йөртелә.

Чыгарылманы исәпләү дифференциал табу дип атала. Кире исәпләү баштагы функцияне табу (русча первообразная) яки интеграл табу дип йөртелә.

Математик тасвиры

Функция чыгарылмасы $~A$ түбәндәгечә күрсәтеп була:

$f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .$

$f(x_{0}+h)=f(x_{0})+Ah+o(h)$

Функция чыгарылмасы чик (lim) ярдәмендә болай күрсәтелә:

$f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .$

$f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}.$

Чыгарылмалар җәдвәле

Дәрәҗәле функцияләр чыгарылмалары	Тригонометрик функцияләр чыгарылмалары	Кире тригонометрик функцияләр чыгарылмалары
$\left(c\right)'=0$	$\left(\sin x\right)'=\cos x$	$\left(\arcsin x\right)'={\dfrac {1}{\sqrt {1-x^{2}}}}$
$\left(x^{a}\right)'=ax^{a-1}$	$\left(\cos x\right)'=-\sin x$	$\left(\arccos x\right)'=-{\dfrac {1}{\sqrt {1-x^{2}}}}$
$\left(a^{x}\right)'=a^{x}\ln a$	$\left(\mathrm {tg} \,x\right)'={\dfrac {1}{\cos ^{2}x}}$	$\left(\mathrm {arctg} \,x\right)'={\dfrac {1}{1+x^{2}}}$
$\left(\log _{a}x\right)'={\dfrac {1}{x\ln a}}$	$\left(\mathrm {ctg} \,x\right)'=-{\dfrac {1}{\sin ^{2}x}}$	$\left(\mathrm {arcctg} \,x\right)'=-{\dfrac {1}{1+x^{2}}}$

$\left(c\right)=\left(const\right)$
$\left(e^{x}\right)^{\left(n\right)}=e^{x}$

Геометрик мәгънә

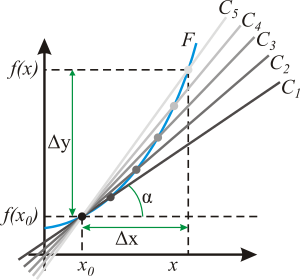Функция чыгарылмасының геометрик мәгънәсе

Әгәр функция ноктада чикле чыгарылмасына ия була икән, димәк ноктаның тирә-ягында функция сызык функциясе белән якынча тасвирланып була:

$f_{l}(x)\equiv f(x_{0})+f'(x_{0})(x-x_{0}).$

Функция $f_{l}$

$f_{l}$ - орынма дип йөртелә

$~f'(x_{0})$ - орынма почмак коэффициенты яки авышлык почмагының тангенсы

Функция чыгарылмасы функциянең мизгелдәге үзгәреш тизлеге булып тора:

$v(t_{0})=s'(t_{0})$

Югары буын чыгарылмалар

$f^{(0)}(x_{0})\equiv f(x_{0}).$

$f^{(1)}(x_{0})\equiv f'(x_{0}).$

$f^{(n+1)}(x_{0})=\left(f^{(n)}\right)'(x_{0}).$

Бүленмә чыгарылма

Күп аргументлы функция

$~u=f(x,y,z)$

бүленмә чыгарылма

$~u''_{x^{2}}=f''_{x^{2}}(x_{0},y_{0},z_{0})$  яки $~{\frac {\partial ^{2}u}{\partial x^{2}}}={\frac {\partial ^{2}f(x_{0},y_{0},z_{0})}{\partial x^{2}}}$

$~u''_{xy}=f''_{xy}(x_{0},y_{0},z_{0})$  яки $~{\frac {\partial ^{2}u}{\partial x\partial y}}={\frac {\partial ^{2}f(x_{0},y_{0},z_{0})}{\partial x\partial y}}$

$~u''_{xy}=f''_{xy}(x_{0},y_{0},z_{0})$

Мисаллар

• $f(x)=x^{2}$. димәк

$f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {x^{2}-x_{0}^{2}}{x-x_{0}}}=\lim \limits _{x\to x_{0}}{\frac {(x-x_{0})(x+x_{0})}{x-x_{0}}}=\lim \limits _{x\to x_{0}}(x+x_{0})=2x_{0}.$

• $f(x)=|x|$. Әгәр $x_{0}\neq 0,$ димәк

$f'(x_{0})=\operatorname {sgn} x_{0},$

биредә $\operatorname {sgn}$ - тамга функциясе. Әгәр $x_{0}=0,$ димәк $f'_{+}(x_{0})=1,\;f'_{-}(x_{0})=-1,$ шуңа күрә $f'(x_{0})$ булмый.

Дифференциал табу кагыйдәләре

• $C'=0$
• $x'=1$
• $\left(f+g\right)'=f'+g'$
• $\left(fg\right)'=f'g+fg'$
• $\left(Cf\right)'=Cf'$
• $\left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}$ …(g ≠ 0)
• $\left({\frac {C}{g}}\right)'=-{\frac {Cg'}{g^{2}}}$ (g ≠ 0)
• $\left\{{\begin{matrix}x=x(t),\\y=y(t),\end{matrix}}\;\;t\in \left[T_{1};T_{2}\right]\right.$,

$y'_{x}={\frac {dy}{dx}}={\frac {dy}{dt}}\cdot {\frac {dt}{dx}}=y'_{t}\cdot t'_{x}={\frac {y'_{t}}{x'_{t}}}$

• ${\frac {d}{dx}}f(g(x))={\frac {df(g)}{dg}}\cdot {\frac {dg(x)}{dx}}=f'_{g}g'_{x}$

$(fg)^{(n)}=\sum \limits _{k=0}^{n}{C_{n}^{k}f^{(n-k)}g^{(k)}},$ биредә $C_{n}^{k}$

• $(f(x)^{g(x)})'=f(x)^{g(x)}\left(g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}}\right)(\forall x\in D_{f}:f(x)>0)$

Кайбер функцияләрдән чыгарылмалар

Функция $~f(x)$	$~f'(x)$ чыгарылмасы	Искәрмә
$~x^{\alpha }$	$~\alpha \cdot x^{\alpha -1}$
$~a^{x}$	$~a^{x}\cdot \ln {a}$
$~\log _{a}{x}$	$~{\frac {1}{x\cdot \ln {a}}}$
$~\sin x$	$~\cos x$
$~\cos x$	$~-\sin x$
$~\mathrm {tg} \ x$	$~{\frac {1}{\cos ^{2}{x}}}$
$~\mathrm {ctg} \ x$	$~-{\frac {1}{\sin ^{2}{x}}}$
$~\arcsin {x}$	${\frac {1}{\sqrt {1-x^{2}}}}$
$~\arccos {x}$	$-{\frac {1}{\sqrt {1-x^{2}}}}$
$~\mathrm {arctg} \ x$	$~{\frac {1}{1+x^{2}}}$
$~\mathrm {arcctg} \ x$	$~-{\frac {1}{1+x^{2}}}$
$~\mathrm {sh} \ x$	$~\mathrm {ch} \ x$
$~\mathrm {ch} \ x$	$~\mathrm {sh} \ x$
$~\mathrm {th} \ x$	$~{\frac {1}{\mathrm {ch} ^{2}\ x}}$
$~\mathrm {cth} \ x$	$~-{\frac {1}{\mathrm {sh} ^{2}\ x}}$

Әдәбият

• В. А. Гусев, А. Г. Мордкович «Математика»
• Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
• В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1