Гравитация
| Гравитация | |
 | |
| Кайда өйрәнелә | Бөтендөнья тартылу кануны һәм Гомуми чагыштырмалылык теориясе |
|---|---|
| Ачучы яки уйлап табучы | Исаак Ньютон |
| WordLift сылтамасы | data.thenextweb.com/tnw/entity/gravity[1] |
| Моның каршысы | негравитационная сила[d] |

Гравитация (тартым, тартылу, бөтендөнья тартылышы) (латин теленнән gravitas — "авырлык") (tat.lat. Gravitatsiä) - һәрбер материаль җисемнәр арасында күпьяклы фундаменталь тәэсир итешү. Аз тизлекнең һәм зәгыйфь гравитацион тәэсир итешү якынчалыгында Ньютонның тартылу теориясе белән тасвирлана, гомуми очракта Эйнштейнның Гомуми чагыштырмалылык теориясе белән тасвирлана.
Гравитация - дүрт фундаменталь тәэсир итешүнең иң зәгыйфе. Квант чигендә гравитацион тәэсир итешү гравитациянең квант теориясе белән тасвирланырга тиеш, ләкин шушы теория эшләнмәгән әле.
Зәгыйфь гравитацион кыр[үзгәртү | вики-текстны үзгәртү]
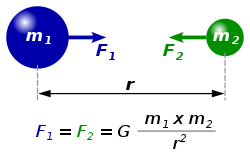
Классик механикада (аз тизлек һәм зәгыйфь гравитация очрагы) гравитацион тәэсир итешү бөтендөнья тартылу кануны белән тасвирлана: ике нокталар арасында M һәм m масса белән һәм R аралыгы белән гравитацион тартым көче ике массага туры пропорциональ һәм аралыкның квадратына кире пропорциональ:
Биредә — гравитацион даими, 6,6725×10−11 м³/(кг·с²).
Гравитация — иң зәгыйфь тәэсир итешү, әмма ул һәрбер ноктада һәм һәр аралыкта тәэсир итә, барлык массалар - уңай, шуңа күрә гравитация Галәмдә бик мөһим көч. Гравитациясез объектлар Галәмдә табылмаган.
Көчле гравитацион кыр[үзгәртү | вики-текстны үзгәртү]

Көчле гравитацион кырда һәм гравитацион кырда релятивистик тизлек белән хәрәкәт иткән очракта Гомуми чагыштырмалылык теориясенең эффектлары күренә:
- фәза-вакытның геометриясенең үзгәреше
- Ньютонның тартылу кануныннан тайпылышы
- экстремаль очракта - кара тишек барлыкка килүе
- потенциалларның кичегүе
- гравитацион дулкыннарның килеп чыгуы
- гравитация үзе белән тәэсир итә башлый, кушу принципы бозыла
Көчле гравитация Эйнштейн тигезләмәсе белән тасвирлана:
(тигезләмәдә: сул якта - геометрия (дүрт үлчәнешле фәза-вакыт), уң якта - матдә)
биредә — Риччи тензоры (фәза-вакытның кәкрәюе тензорыннан килеп чыккан )
— скаляр кәкрәю, - метрик тензор, һәм Риччи тензоры
— космологик даими, - энергия-импульс тензоры, — Пи саны, — вакуумда яктылык тизлеге, — Ньютон гравитацион даимие.
- Эйнштейн тензоры
— Эйнштейн гравитацион даимие.
Искәрмәләр[үзгәртү | вики-текстны үзгәртү]
Әдәбият[үзгәртү | вики-текстны үзгәртү]
- Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). — М.: Наука, 1981. — 352c.
- Визгин В. П. Единые теории в 1-й трети ХХ в. — М.: Наука, 1985. — 304c.
- Иваненко Д. Д., Сарданашвили Г. А. Гравитация. 3-е изд. — М.: УРСС, 2008. — 200с.
- Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977.
- Торн К. Черные дыры и складки времени. Дерзкое наследие Эйнштейна. — М.: Государственное издательство физико-математической литературы, 2009.
















