Wikipedia — ирекле энциклопедия проектыннан ([http://tt.wikipedia.org.ttcysuttlart1999.aylandirow.tmf.org.ru/wiki/Баштагы функция latin yazuında])
 өчен баштагы функцияләр күплеге
өчен баштагы функцияләр күплеге 
 Мәйдан баштагы функцияләр аермасына тигез
Мәйдан баштагы функцияләр аермасына тигез
Баштагы функция (рус. Первообразная, ингл. Antiderivative) — функция интегралын табу өчен кулланыла торган функция.  функциясенең баштагы функциясе дип, чыгарылмасы
функциясенең баштагы функциясе дип, чыгарылмасы  ка тигез булган,
ка тигез булган,  функциясен атыйлар. Ягъни:
функциясен атыйлар. Ягъни:  . Баштагы функцияне табу билгесез интеграл табудан гыйбәрәт һәм бу процесс интеграл табу дип атала.
. Баштагы функцияне табу билгесез интеграл табудан гыйбәрәт һәм бу процесс интеграл табу дип атала.
Мисал:  өчен баштагы функция
өчен баштагы функция  була. Константадан чыгарылма нульгә тигез, шуңа күрә гомуми баштагы функция болай күренә:
була. Константадан чыгарылма нульгә тигез, шуңа күрә гомуми баштагы функция болай күренә:  биредә
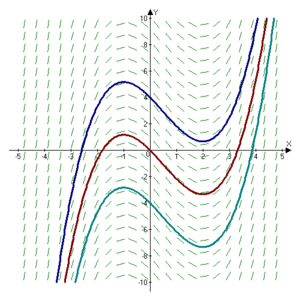
биредә  - теләгән сан. Мондый баштагы функцияләрнең графиклары бер-берсенә карата вертикаль буенча күчкәннәр, һәм бу күчеш
- теләгән сан. Мондый баштагы функцияләрнең графиклары бер-берсенә карата вертикаль буенча күчкәннәр, һәм бу күчеш  даимиенә генә бәйле.
даимиенә генә бәйле.
Ньютон-Лейбниц тигезләмәсе буенча баштагы функцияләр аермасы интегралга тигез:

 функциянең баштагы функцияләре күплеге - билгесез интеграл дип йөртелә, анда чикләр язылмый:
функциянең баштагы функцияләре күплеге - билгесез интеграл дип йөртелә, анда чикләр язылмый:

Һәрбер баштагы функция  өзлексез функциядән
өзлексез функциядән  билгесез интеграл ярдәмендә күрсәтелеп була:
билгесез интеграл ярдәмендә күрсәтелеп була:

Кайбер өзлекле функцияләр баштагы функциягә ия була:
Мисал өчен:  :
: өзлекле
өзлекле  , ләкин баштагы функ.
, ләкин баштагы функ.  с
с  бар
бар
Шулай ук элементар функцияләр ярдәмендә күрсәтелеп булмаган баштагы функцияләр бар:
 .
.




- гомуми очракта,[1]












































- В. А. Гусев, А. Г. Мордкович «Математика»
- Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
- В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1
- ↑ "Reader Survey: log|x| + C", Tom Leinster, The n-category Café, March 19, 2012




































































