Ферми — Дирак бүленеше
Ферми — Дирак бүленеше яки Ферми — Дирак статистикасы (tat.lat. Fermi — Dirak büleneşe(үле сылтама))- ярым бөтен спин белән бертигез кисәкчәләр энергия биеклеге буйлап термодинамик тигезләнештә бүленеше. Ярым бөтен спинлы кисәкчәләр фермион дип исемләнә, мәсәлән: электрон (1/2 спин), протон (1/2 спин) һәм бүтән. Фермионнар Паули мәсләгенә буйсыналар: ике һәм күбрәк фермион (ярым бөтен спин белән кисәкчек) бер квант халәттә була алмый.
Ферми — Дирак бүленеше 1926 елда итальян галим Энрико Ферми һәм инглиз физигы Поль Дирак тарафыннан тәкъдим ителгән.
Ферми — Дирак һәм Бозе — Эйнштейн бүленешләре квант күренешләрен исәпкә ала. Квант тәэсире (N/V) ≥ nq тупланышында барлыкка килә.
- nq — квант тупланыш: кисәкчәләр арасында ераклыгы кисәкчәләр Де-Бройль дулкыны озынлыгына тигез.
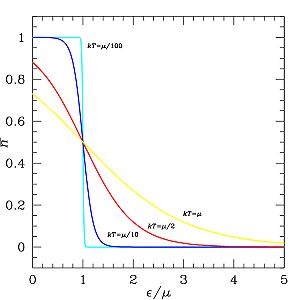
Ферми — Дирак бүленеше әлеге квант дәрәҗәсендә фермион булуының ихтималлыгын тасвирлый.
Уртача кисәкчәләр саны энергиясе белән :
- — хәлендә урта кисәкчәләр саны,
- — - хәленең энергиясе,
- — -хәленең бозылуы (-энергиясе белән халәтләр саны),
- — химик потенциал (нуль теспературасында - Ферми дәрманына тигез),
- — Больцман даимие,
- — абсолют температура
Идеаль ферми-газда түбән температурасында . Бу очракта (энергия дәрәҗәләре тәлгәшләнмәгән очракта) бүленеш функциясе - Ферми - функциясе дип исемләнә:
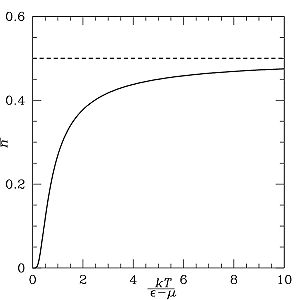
Температураның йогынтысы
[үзгәртү | вики-текстны үзгәртү]Химик потенциал температурага бәйле. Әгәр системаның температурасы - Ферми температурасыннан түбәнрәк булса якынчалык кулланыла:
Чынлыкта:
Кулланыш
[үзгәртү | вики-текстны үзгәртү]Ферми — Дирак бүленеше электр үткәрүчәнлеген, Ферми өслеген тасвирлый.
Моны да карагыз
[үзгәртү | вики-текстны үзгәртү]- Бозе — Эйнштейн тупланышы
- Людвиг Больцман
- Үтә үткәрүчәнлек
- Гаусс бүленеше
- Пуассон бүленеше
- Максвелл — Больцман бүленеше
Әдәбият
[үзгәртү | вики-текстны үзгәртү]- Бозе — Эйнштейна статистика // Большая советская энциклопедия: В 30 т. / Главный редактор А. М. Прохоров. — 3-е издание. — М.: Советская энциклопедия, 1970. — Т. 3. Бари — Браслет. — 640 с.














![{\displaystyle \mu =E_{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {k_{B}T}{E_{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {k_{B}T}{E_{F}}}\right)^{4}+\ldots \right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11976130f37c2e8e7c17ad94590c8c4b578cf64e)